Top Links
Journal of Veterinary Science and Animal Husbandry
ISSN: 2348-9790
Multivariate Multiple Regression Models Based on Principal Component Factor Scores to Predict Bodyweight from Morphometric Traits in a Population of Indigenous Sheep in Ethiopia
Copyright: © 2023 Kefelegn Kebede. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Related article at Pubmed, Google Scholar
This study aimed at assessing variability among morphometric traits, deducing components that describe these traits and predicting bodyweight from both original and orthogonal traits using regression models. Bodyweight and fifteen morphometric traits namely height-at-whither (HW), body-length (BL), chest-depth (CD), chest-girth (CD), rump-length (RL), rump-height (RH), pelvic-width (PW), shoulder-width (SW), head-width (HdW), head-length(HdL), cannon-bone-length (CBL), cannon-bone-circumference (CBC), ear-length (EL), horn-length (HL), tail-length (TL), and tail-circumference (TC) were recorded on 600 extensively managed and randomly selected adult sheep
Keywords: Morphometric traits; Multivariate analysis; Principal component factor analysis; Sheep
Ethiopia is endowed with many livestock species with an estimated population of 62.6 million cattle, 31.7 million sheep, 33.0 million goats, and 61.5 million poultry [1] Sheep production is one of the most widespread of animal husbandry systems in Ethiopia. Sheep is a multi-functional animal and plays a significant role in the economy and nutrition of resource poor farmers. Indigenous sheep in Ethiopia are well adapted to the various agro-ecological zones of the country [3,4]. Their adaptability across the different agro-ecological zones depicts a repository of genetic diversity, possession of gene combinations and distinctive adaptation traits such as disease resistance, and effective utilization of poor-quality forages [5,6].
Despite having these specific utilities in their native tract, in the last few decades, there is a marked decline in their population due to widespread use of crossbreeding, destruction of the traditional production system, and general thrust towards high input management system. To prevent the rich biological heritage from genetic erosion, it is imperative to redefine the breeding strategies and conservation programs.
To a sustainable use of animal genetic resources, the characterization of a breed of livestock is the first approach [7]. Livestock conformation appraisal has remained the oldest means of generating information and has been used with great success over the years, it is also vital in contrasting size and shape of animal [8,9].
In any livestock enterprise, body weight is a crucial piece of information that a producer needs to know to make proper management decisions (feeding and breeding management, marketing, health care, choosing replacement males and females etc.). Without an accurate measurement of body weight, making sound management decisions is daunting, if not impossible [10-12]. The increasing need to estimate the body weight of animals to study their growth pattern has led to the development of multiple linear regression (MLR) equations which were designed to predict the body weight of from morphometric traits [13-15]. However, the biological interpretation of results obtained from MLR analysis may be misleading because of the existence of a high correlation (multi-collinearity problem) between the predictors that yields a deficiency in the regression model obtained [14][16]. One of the approaches used to avoid this problem is the application of principal component (PC) factor analysis [17][9]. PC factor scores derived from PC factor analysis offers the opportunity to estimate body weight with a high degree of accuracy and solving the problem of multi-collinearity. In sheep breeding, the identification of multivariate inter-relationships among bodyweight and morphometric traits is necessary for selecting better animals with the aim of gaining more genetic progress on animal performance.
In Ethiopia, inter-relationship among morphometric traits of livestock treated as multivariate (analyzed simultaneously) have not been widely exploited. Therefore, the present investigation makes use of PC factor analysis to assess variability among morphometric traits, deduce components that describe these traits and predict bodyweight from both original and orthogonal traits.
The study was conducted in three districts (Damote-Sore, Damote-Gale, and Sodo- Zuria) of Wolaita Zone of the Southern Nations, Nationalities and Peoples Regional state of Ethiopia. The three districts were purposively selected based on sheep population potential and road accessibility. The capital town of the zone, Wolaita Soddo, is located 330 km away from Addis Ababa. Wolaita Soddo is located at 6.51 - 7.35 N latitude and 37.23 - 38.14 E longitudes.
A total of 630 sheep (210 sheep (62 males and 148 females) from Damote-Sore, 210 sheep (132 males and 78 females) from Damote-Gale 210 sheep (75 males and 135 females) from Sodo-Zuuria) were randomly selected and used for physical measurements. Bodyweight (BW) and morphometric traits namely height-at-whither (HW), body-length (BL), chest-depth (CD), chest-girth (CG), rump-length (RL), rump-height (RH), pelvic-width (PW), shoulder- width (SW), head-width (HW), head-length (HL), cannon-bone-length (CBL), cannon-bone- circumference (CBC), ear-length (EL), horn-length (HL), tail-length (TL), and tail-circumference (TC) were recorded following the recommended FAO descriptors for sheep genetic resources (FAO, 2012). Measuring tapes and a suspended spring balance were used to measure the respective morphometric traits and body weight of sheep.
All statistical analyses were performed using the SAS 9.4 software (version 9.4; SAS Institute Inc., NC). In livestock, such studies are mainly carried out on females due to their larger numbers [19][20][11]. Thus, in this study, in order to avoid potential sampling bias due to low number of males, only females were considered in the analysis.
The body weight and morphometric traits were subjected to exploratory data analysis to get results of descriptive statistics and correlation matrices using the PROC UNIVARIATE and PROC CORR procedures of SAS (version 9.4; SAS Institute Inc., NC).
Estimating the number of PCs: Several criteria are available for determining the number of PCs to be extracted. In this study, the criteria Kaiser–Guttman rule, the scree test, and parallel analysis plot were used.
Kaiser–Guttman rule:This rule states that the number of PCs to be extracted should be equal to the number of PCs having an eigenvalue greater than 1. An eigenvalue greater than 1 indicates that PCs account for more variance than accounted for by one of the original traits in standardized data. Eigenvalues measure the amount of the variation explained by each PC and will be largest for the first PC and smaller for the subsequent PCs.
Scree test:Plotting the eigenvalues against the corresponding PC produces a screen plot that illustrates the rate of change in the magnitude of the eigenvalues for an increasing number of PCs. The rate of decline tends to be fast first and then levels off. The “elbow,” at which the curve bends, is considered to indicate the maximum number of PCs to extract.
Parallel analysis:To aid the decision making in the selection of the number of PCs extracted, a graphical method known as parallel analysis is suggested to enhance the interpretation of the scree plot. The optimum number of PCs is selected at the cut-off point, where the scree plot and the parallel analysis curve intersect.
PC loading:They are correlation coefficients between the PC scores and the original traits. A high positive correlation between PC1 and a trait indicates that the trait is associated with the direction of the maximum amount of variation in the dataset. A strong correlation between a trait and PC2 indicates that the trait is responsible for the next largest variation in the data perpendicular to PC1, and so on.
Multiple linear regression procedure was used to obtain models for predicting body weight from morphometric traits (a), and from PC factor scores (b)
where, BW is the body weight, „bo is the intercept, b1 is the ith partial regression coefficient of the ith morphometric trait, Xi or the ith PC.
Table 1 shows the mean±standard error, standard deviation, coefficient of variation, minimum, and maximum estimates of body weight and morphometric traits of the indigenous sheep.
The mean body weight was 25.2 kg while the morphometric traits were 70.5 cm (HG), 63.3 cm (HW), 63.6 cm (BL), 17.0 cm (PW), 16.5 cm (SW), 29.7 cm (CD), 9.2 cm (HdW), 18.0 cm (HdL), 16.0 cm (CbL), 9.7 cm (CbC), 29.7 cm (TL), 17.2 cm (TC), 65.4 cm (RH), 19.7 cm (RL), and 10.5 cm (EL) respectively. Rump length varied most (CV = 40.4 %) while height at withers (CV = 5.8 %) varied the least. The descriptive statistics results found in this study agree with earlier reports by Bosenu et al. (2014) and Ahmed et al. (2015).
The degree of linear association among the morphometric traits measured by the Pearson correlation coefficient (r) and their statistical significance are presented in table 2. The correlation coefficients varied from 0.11 (between RL and PW) to 0.97 (between HG and BL and between BW and HG). Among 107 possible pairs of correlations, all pairs of correlations were found significant, indicating that the data is suitable for performing PCA. Such positive and significant correlation coefficient values have also been reported in sheep by the studies of Bosenu et al. (2014) and Ahmed et al. (2015). Positive correlations suggest that selection for a trait also lead to a correlated response in the other trait, thus providing a basis for the genetic manipulation and improvement of animals.
* significant at p 0.05 for all correlation coefficients; Bodyweight (BW); heart-girth (HG); height-at-whither (HW); body-length (BL); chest-depth (CD); chest-girth (CG); rump-length (RL); rump-height (RH); pelvic-width (PW); shoulder-width (SW); head-width (HdW); head- -length (HdL); cannon-bone-length (CbL); cannon-bone-circumference (CbC); ear-length (EL); horn-length (HL); tail-length (TL); and tail-- circumference (TC).
Table 2: Phenotypic correlations and their statistical significance levels among body-weight and morphometric traits of sheep* .
Anti-image correlations computed showed that partial correlations were low, indicating that true factors existed in the data. This was further supported by Kaiser-Meyer-Olkin (KMO) measure of sampling adequacy studied from the diagonal of partial correlation, revealing the proportion of the variance in the body measurements caused by the underlying factor. This was found to be sufficiently high with a value of 0.91 [16] reported that a KMO measure of 0.60 and above is considered adequate. Bartlett’s sphericity test for testing the null hypothesis that the correlation matrix is an identity matrix was used to verify the applicability of PCA. The value of Bartlett’s sphericity test was significant (p-value = 0.001), implying that the PCA is applicable to the data set.
Table 3 presents the eigenvalue of the total variance, the rotated component matrix and communalities of the traits investigated. The table shows how much of the total variance of the observed traits is explained by each of the PCs after varimax rotation of the component matrix. Two PCs were identified with eigenvalues of 11.1 (PC1) and 1.2 (PC2). PC1 explained 74.3 % of the total variance while PC2 explained only 8.1 %. Accordingly, the first two PC factors combined accounted for 82.4 % of the total variability present in the parameters measured. The communalities are the proportion of variance that each trait has in common with other traits. Thus, if communality of a trait is high, it means that the extracted factors explained a big proportion of the variance the trait. The communality values ranged from 0.19 (RL) to 0.96 (TL) indicating that the data are conformable to PC factor analysis.
PC loadings presented in table 3 are the correlation coefficient between the first two PC scores and the original traits. They measure the importance of each morphometric trait in accounting for the variability in the PC. That is, the larger the loadings in absolute terms, the more influential the variables are in forming the new PC and vice versa. The first factor (PC1) loaded heavily on TL, PW, HdL, TC, HG, RH, BL, CC, HdW, CL, SW, HW, EL and CD while the second factor (PC2) loaded heavily on HdL, TC, HG, RH, BL, CC, HdW, CL, SW, HW, EL, CD and RL. The loading classification found in this study is somewhat similar to those reported by Uda [9], and immature Uda [21].
A scree-parallel analysis plot of eigenvalues against their PCs is shown in figure 2 below. The plot demonstrates the distribution of variance among the components graphically. For each PC, the corresponding eigenvalue is plotted on the y-axis. By definition, the variance of each component is less than the preceding one. Here there appears to be a marked decrease in downward slope after the second PC implying that one can summarize the nine morphometric traits by the first two PCs
The interdependent original morphometric traits and their independent PC factor scores were used to the predict body weight of sheep. Table 4 presents the regression coefficient, their standard errors, t-value, p-values, variance inflation factor (VIF) values, and R2 adjusted obtained from MLR analysis. The regression of body weight on HG, BL, SW, CD, HdW, CC, TL, TC, and RH was significant, while it was not significant for HW, PW, HdL, CL, RL, and EL. The present findings are consistent with the submissions of [22] in sheep and [23] in goats.
Heart girth (HG); height-at-whither (HW); body-length (BL); chest-depth (CD); chest-girth (CG); rump-length (RL); rump-height (RH); pelvic-width (PW); shoulder-width (SW); head-width (HW); head-length (HL); cannon-bone-length (CBL); cannon-bone-circumference (CBC); ear-length (EL); horn-length (HL); tail-length (TL); and tail-circumference (TC).
Table 4: MLR of body weight on original morphometric traits and their PC factor scores
To increase the meat yield and carcass production of sheep, the genetic improvement of body weight is necessary and this requires adequate knowledge of correlated traits that can be considered when selection is to be applied. However, the use of interdependent predictors should be treated with caution, since multicollinearity is associated with unstable estimates of regression coefficients [24-26] rendering the estimation of unique effects of these predictors impossible. This is evident in the present study, where HG, HW, BL, PW, SW, HdW, CC, TL, TC, RH, and RL having VIF values greater than 10. [27] stated that VIF values above 10 indicate severe collinearity which leads to unstable estimation of the associated least square regression coefficient. To overcome this limitation, the use of PC factor scores for prediction of body weight as predictors is used [28] [17] [9]. These PCs are orthogonal to each other and are more reliable in weight estimation. In the present study, the use of PC1 and PC2 together accounted for 92 % of the variation in body weight of the chickens. The two factors selected were found to have significant positive linear relationship with body weight (Table 4). In other words, body weight will be expected to increase as the values of factor 1 and 2 scores increase.
Similarly, [29] derived regression equations for estimating body weight of sheep using independent factor scores. In another related study, [30] obtained a single linear model involving principal component scores and capture methods and sex of musk ducks; while [28] used factor scores derived from ten body measurements to predict the carcass weight of sheep.
This study revealed through Pearson correlation coefficients that great and predictive degree of relationship existed amongst morphometric traits. PC factor analyses was explored in identifying patterns and explore the inter-dependence in sixteen morphometric traits of indigenous sheep to eliminate redundancy and predict body weight. The technique extracted two PCs that could aid in selection and breeding programmes. The traits accounted for PC1 included HdL, TC, HG, RH, BL, CC, HdW, CL, SW, HW, EL, CD and RL; while for PC2 the corresponding traits were HdL, TC, HG, RH, BL, CC, HdW, CL, SW, HW, EL, CD and RL. The use of independent orthogonal indices (PC1 and PC2) derived from PC factors’ score was more appropriate than the use of original interrelated morphometric traits for predicting the body weight of ewes, as multi-collinearity problems were handled and removed. The two factors extracted from the present investigation could be used to select animals based on a group of variables rather than isolated traits. PC factor analysis can therefore be applied in the ranking of animals based on different indices thus aiding in the drastic reduction of the number of morphometric traits required for selection in a breeding programme for improvement and performance of sheep
 |
| Figure 1: Map of the study area |
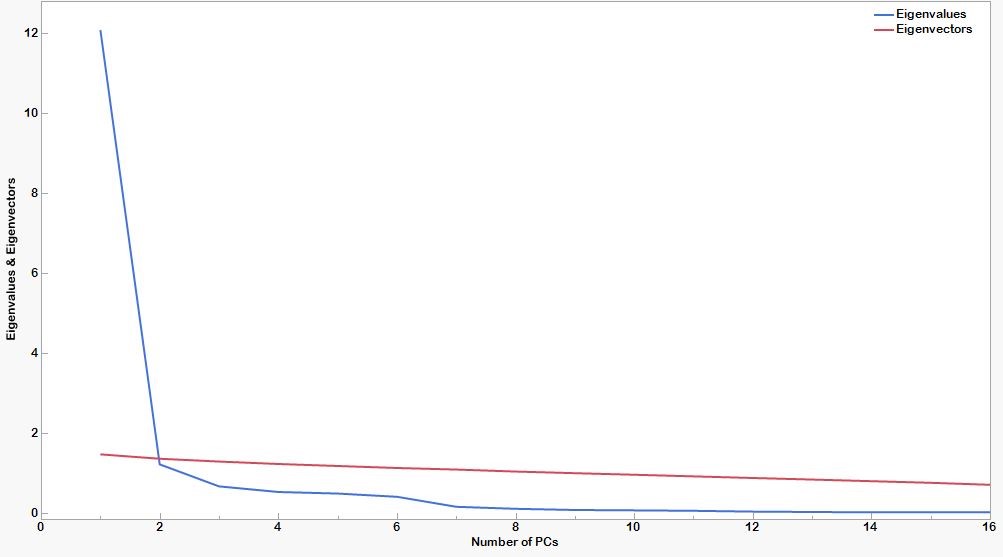 |
| Figure 2: Scree and parallel analysis plots. |
Nr. |
Trait (unit) |
Label |
Mean ± SE |
STD |
CV |
Min. |
Max. |
1 |
Body weight (kg) |
BW |
25.2±0.3 |
4.9 |
19.3 |
15 |
34 |
2 |
Heart girth (cm) |
HG |
70.5±0.3 |
4.9 |
6.9 |
58 |
78 |
3 |
Height at withers (cm) |
HW |
63.3±0.2 |
3.7 |
5.8 |
55 |
70 |
4 |
Body length (cm) |
BL |
63.6±0.2 |
4.2 |
6.6 |
52 |
70 |
5 |
Pelvic width (cm) |
PW |
17.0±0.1 |
2.1 |
12.6 |
14 |
22 |
6 |
Shoulder width (cm) |
SW |
16.5±0.1 |
1.6 |
9.9 |
13 |
20 |
7 |
Chest depth (cm) |
CD |
29.7±0.2 |
4.3 |
14.5 |
3 |
36 |
8 |
Head width (cm) |
HdW |
9.2±0.1 |
1.4 |
14.9 |
6 |
12 |
9 |
Head length (cm) |
HdL |
18.0±0.1 |
1.7 |
9.2 |
15 |
21 |
10 |
Cannon bone length (cm) |
CBL |
16.0±0.1 |
1.2 |
7.6 |
13 |
19 |
11 |
Cannon bone circumference (cm) |
CBC |
9.7±0.1 |
1.7 |
17.9 |
6 |
12 |
12 |
Tail length (cm) |
TL |
29.7±0.2 |
4.1 |
13.8 |
24 |
38 |
13 |
Tail circumference (cm) |
TC |
17.2±0.2 |
3.0 |
17.7 |
10 |
24 |
14 |
Rump height (cm) |
RH |
65.4±0.2 |
3.9 |
5.9 |
54 |
72 |
15 |
Rump length (cm) |
RL |
19.7±0.4 |
8.0 |
40.4 |
2 |
85 |
16 |
Ear length (cm) |
EL |
10.5±0.1 |
0.9 |
8.2 |
9 |
12 |
Trait |
BW |
HG |
HW |
BL |
PW |
SW |
CD |
HdW |
HdL |
CbL |
CbC |
TL |
TC |
RH |
RL |
EL |
BW |
1.00 |
|
|
|||||||||||||
HG |
0.97 |
1.00 |
|
|||||||||||||
HW |
0.93 |
0.90 |
1.00 |
|
||||||||||||
BL |
0.96 |
0.97 |
0.91 |
1.00 |
|
|||||||||||
PW |
0.81 |
0.79 |
0.73 |
0.75 |
1.00 |
|
||||||||||
SW |
0.88 |
0.83 |
0.90 |
0.83 |
0.78 |
1.00 |
|
|||||||||
CD |
0.60 |
0.55 |
0.57 |
0.55 |
0.45 |
0.61 |
1.00 |
|
||||||||
HdW |
0.86 |
0.82 |
0.91 |
0.82 |
0.73 |
0.92 |
0.60 |
1.00 |
|
|||||||
HdL |
0.88 |
0.88 |
0.84 |
0.86 |
0.89 |
0.82 |
0.56 |
0.79 |
1.00 |
|
||||||
CbL |
0.77 |
0.72 |
0.79 |
0.70 |
0.65 |
0.89 |
0.63 |
0.86 |
0.76 |
1.00 |
|
|||||
CbC |
0.84 |
0.78 |
0.90 |
0.78 |
0.65 |
0.90 |
0.61 |
0.93 |
0.72 |
0.84 |
1.00 |
|
||||
TL |
0.84 |
0.83 |
0.77 |
0.81 |
0.94 |
0.76 |
0.50 |
0.73 |
0.91 |
0.63 |
0.63 |
1.00 |
|
|||
TC |
0.90 |
0.86 |
0.88 |
0.83 |
0.84 |
0.86 |
0.60 |
0.85 |
0.89 |
0.81 |
0.78 |
0.88 |
1.00 |
|
||
RH |
0.96 |
0.97 |
0.90 |
0.96 |
0.80 |
0.84 |
0.58 |
0.82 |
0.88 |
0.74 |
0.78 |
0.83 |
0.87 |
1.00 |
|
|
RL |
0.34 |
0.30 |
0.37 |
0.29 |
0.11 |
0.36 |
0.33 |
0.35 |
0.21 |
0.37 |
0.39 |
0.20 |
0.40 |
0.31 |
1.00 |
|
EL |
0.65 |
0.61 |
0.66 |
0.60 |
0.49 |
0.69 |
0.53 |
0.72 |
0.63 |
0.73 |
0.62 |
0.54 |
0.69 |
0.64 |
0.35 |
1.00 |
Trait |
PC1 |
PC2 |
Communalities |
Heart girth (cm) |
0.742 |
0.563 |
0.87 |
Height at withers |
0.612 |
0.737 |
0.92 |
Body length |
0.709 |
0.585 |
0.84 |
Pelvic width |
0.899 |
0.289 |
0.89 |
Shoulder width |
0.591 |
0.746 |
0.91 |
Chest depth |
0.356 |
0.536 |
0.41 |
Head width |
0.535 |
0.796 |
0.92 |
Head length |
0.852 |
0.432 |
0.91 |
Cannon bone length |
0.457 |
0.762 |
0.78 |
Cannon bone circumference |
0.418 |
0.860 |
0.91 |
Tail length |
0.941 |
0.270 |
0.96 |
Tail circumference |
0.760 |
0.558 |
0.89 |
Rump height |
0.736 |
0.576 |
0.87 |
Rump length |
0.068 |
0.434 |
0.19 |
Ear length |
0.401 |
0.597 |
0.52 |
Eigenvalue |
11.1 |
1.2 |
|
% of total variance |
74.3 |
8.1 |
82.46 |
Model |
Coefficient |
SE |
t-value |
p-value |
VIF |
|
Original morphometric traits as predictors |
||||||
Intercept |
-38.3 |
2.3 |
-16.5 |
<.0001 |
. |
|
HG |
0.46 |
0.05 |
9.8 |
<.0001 |
27.7 |
|
HW |
0.06 |
0.05 |
1.1 |
0.2730 |
20.6 |
|
BL |
0.12 |
0.06 |
2.1 |
0.0406 |
32.1 |
|
PW |
-0.02 |
0.09 |
-0.2 |
0.8517 |
20.7 |
|
SW |
0.35 |
0.10 |
3.42 |
0.0007 |
14.8 |
|
CD |
0.04 |
0.01 |
2.54 |
0.0114 |
2.0 |
|
HdW |
-0.39 |
0.13 |
-3.04 |
0.0026 |
15.9 |
|
HdL |
-0.15 |
0.10 |
-1.57 |
0.1177 |
13.7 |
|
CL |
-0.20 |
0.11 |
-1.82 |
0.0691 |
9.2 |
|
CC |
0.49 |
0.10 |
5.12 |
<.0001 |
14.5 |
|
TL |
0.10 |
0.05 |
2.04 |
0.0426 |
20.7 |
|
TC |
0.16 |
0.05 |
3.03 |
0.0026 |
13.5 |
|
RH |
0.16 |
0.05 |
2.96 |
0.0033 |
22.3 |
|
RL |
0.00 |
0.01 |
0.44 |
0.6638 |
1.76 |
|
EL |
0.12 |
0.09 |
1.37 |
0.1720 |
3.09 |
|
|
R2 adjusted = 0.97 |
|||||
Orthogonal morphometric traits as predictors |
||||||
Intercept |
25.2 |
0.07 |
347.23 |
<.000 |
. |
|
PC1 |
3.5 |
0.07 |
47.6 |
<.000 |
1.0 |
|
PC2 |
3.1 |
0.08 |
41.2 |
<.000 |
1.0 |
|
|
R2 adjusted = 0.92 |
|||||






































