Top Links
Journal of Energy Resources and Conversion
Adsorption Kinetics and Mass Balance Mathematical Model of Monoethanolamine Surface-Modified Palm Shell Activated Carbon for Carbon Dioxide Dynamic Adsorption in Fixed Bed Column
Copyright: © 2021 Khalil SH. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Related article at Pubmed, Google Scholar
Dynamic adsorption kinetics results indicated that monoethanolamine-carbon dioxide (MEA-CO2) reaction in fixed bed column packed with MEA-impregnated activated carbon (AC) particles is pseudo first order reaction. The controlling step (slow step) of adsorption is the mass transfer of CO2 molecules form the feed gas bulk stream to the surface of the adsorbent through the boundary layer (external diffusion). A Dubinin-Astakhov and Avrami models showed that adsorption of CO2 on MEA-impregnated activated carbon particles is homogeneous. The suggested mass balance model exhibited good agreement with the experimental results for both MEA-impregnated and non-impregnated AC, which they show also that there is no difference in adsorption rates between the two adsorption beds.
Keywords: Adsorption Kinetics; Activated Carbon; Impregnation; MEA
The removal of carbon dioxide (CO2) is significant for oil and gas industry due to its harmful acidic effects on oil and gas pipelines with no added energy value to natural gas [1]. Because of the increasing indications of CO2 implication in global warming [2], capturing CO2 from its emitting sources is becoming a vital topic. Adsorption is offering an effective alternative for CO2 capturing comparing to other capture technologies [3]. There are many types of gas adsorbents; conventional, like, activated carbons, silica gel, ion-exchange resins, zeolites, and meso-porous silicates, activated alumina, metal oxides, and new like, carbon fibers and metalorganic frameworks [4]. Adsorbent most important feature is adsorbing capacity [5], besides, good adsorbent should be selective and chemically and mechanically durable [6]. AC is cost-effective and adaptable microporous adsorbent [7] and is considered a superb adsorbent due to its high specific surface area, appropriate pore size distribution, diversity of surface chemistry [8]. It’s mostly micropore structure were used extensively in liquids and gases systems. The micropores and mesopores of the AC particles were utilized to accommodate the impregnating molecules, which can be attached chemically (grafting) or physically (impregnation) to the AC particles [9]. Impregnation of AC particles with chemicals improves their natural adsorption capability to adsorb gases [10]. Alkanolamines, such as, monoethanolamine (MEA), diethanolamine (DEA), and methyldiethanolamine (MDEA) are very important absorbents for acidic gases in the field of natural gas sweetening and for mitigation the adversity of these gases on environment [11] and they are extensively used in CO2 absorption from different gas sources [12]. MEA, which is a primary amine, has been used intensively to capture CO2 from gas streams and from many various sources due to its fast reaction kinetics with CO2,low coast and thermal stability, as it is more favorable than other alkanolamines [13,14]. Because of the effectiveness of liquid amine absorption process researchers were encouraged to utilize amines in their solid state for CO2 capture [15]. Adsorption kinetics is essential tool used to evaluate the performance of an adsorbent and to understand the mechanism of adsorption [16] and many researches had included kinetics of batch CO2 adsorption on different adsorbents in their works [17]. They found that the restriction step is the intraparticle diffusion (pore diffusion). On contrary to the findings of this paper where the restrictive step to CO2 adsorption was the film diffusion. In this research, dynamic adsorption experiments were conducted to investigate the adsorption kinetics of MEAimpregnated AC particles packed in adsorption column to adsorb CO2 from gas mixture.
1. Certified analytical reagent monoethanolamine (MEA), C2H7NO, molecular weight 61.
2. Commercial palm shell AC was purchased from Bravo Green SDN BHD
(Sarawak, Malaysia).
3. Gases
a. Mixture of 15% CO2 with 85% N2.
b. Pure N2.
AC particles characterization:Granulated palm shell AC particles were physically activated by steam. The mostly micropore particles have total Bet surface area of 838 cm2/g, while the micropore surface area of that total area is 675 cm2/g and micropore volume is 0.32 cm3/g.
AC beds perpetration:A household coffee grinder crushed the AC particles. 710 and 500 µm sieves were employed to characterize the AC particles to the required particle size of 500 µm (particles passing 710 and stopping on 500 µm sieve).
Impregnation of AC samples:Impregnation was carried out by placing 5 g of granular AC in a beaker, 2 g of MEA added to the beaker with 10 g of deionized water as an environmentally friendly medium and to facilitate the impregnation process. The beaker contents were stirred at 500 rpm for 1 hour at room temperature. The final slurry then dried completely in Heraeus Instrument Vacuthermo oven at 70 oC under 0.1 bar vacuum pressure (absolute) for 6 hours. Samples of AC particles prepared for CO2 adsorption separation experiments are, non-impregnated AC particles and MEA-impregnated AC particles.
Working breakthrough time:Working breakthrough time was utilized as a method to evaluate the performance of AC beds. Breakthrough time can be defined as the time spanning from the beginning of the adsorption experiment to the point when CO2 molecules start to break through out of the adsorption column, which was monitored by Guardian plus CO2 monitor. Data Acquisition Logger was connected to the CO2 monitor to measure the breakthrough time in minutes.
Experimental setup is presented in another work [18].
Amines remove CO2 in a two-step process:
1. The gas absorbs by the liquid forming a weak acid
2. The weak acid reacts with amines as a weak base [19].
The suggested [20] reaction path of primary and secondary unhindered amines with CO2 is known as the carbamate formation reaction proceeds through the formation of zwitterion, which was recognized as the reaction mechanism [21].
The first step of the reaction is the formation of amine-CO2 zwitterion as shown in Equation 1a:
The second step is the deprotonation of the zwitterion. For liquid amine reaction, the water would act as a base acquiring the proton released by the zwitterions. In the case of solid amine reaction, another amine molecule would acquire the released proton as the maximum theoretical amount of CO2 reacting with amine would be 0.5 mol CO2/1 mol N2 as shown in equation 1. In this step, the zwitterion would be stabilized by producing carbamate as in equation 1b
The overall reaction is as in equation 1:
Rate and mechanism of adsorption: To investigate the rate of adsorption two equations were explored namely, pseudo first order (SFO) and pseudo second order (PSO) equations. The mechanism of adsorption and the adsorption controlling step was determined by Weber-Morris intraparticle diffusion model.
MEA molecules occupied the pores of the mostly micropore AC particles and blocked them, reducing significantly the micropore surface area from 675 to 36 m2/g (96%) and micropore volume from 0.32 to 0.02 cm3/g (94%). MEA-blocked AC particles adsorb selectively more CO2 comparing to non-impregnated AC particles by 172%, as the adsorption capacity increased from 49 to 18mg/g, respectively.
Adsorption rate:Pseudo first and second order models were investigated to find out which model is predicting the adsorption rate appropriately.
Lagergren [22] published his SFO model to describe homogenous adsorption on solid phase as in equation 2. The equation depends on the adsorption capacity of an adsorption bed rather than concentration of adsorbate as in the case of first order model equation and the adsorption rate is related to the availability of adsorption sites [23]. It had been reported that SFO model can be applied adequately for the adsorption kinetics of CO2 on AC [24].
The linear form of equation 1 is as in equation 3:
Where,
qe: Adsorption capacity at equilibrium, mg/g
qt: Adsorption capacity at any time t, mg/g
k1: Pseudo-first order rate constant, 1/min
t: Time, min
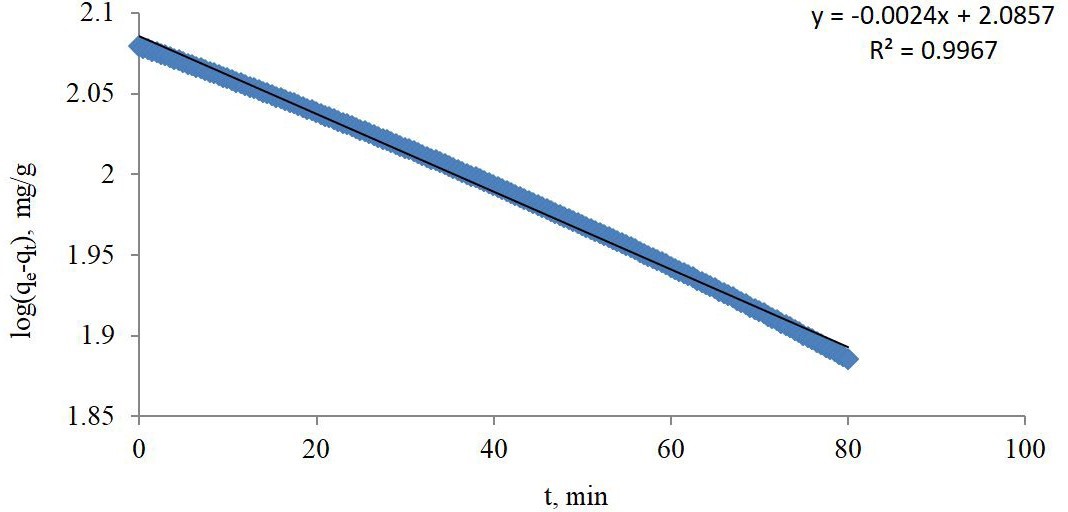
Figure 1 is a plot of ln (qe-qt) against t for the whole adsorption experiment showing that the straight line fitting the experimental results has good value of R2 equal to 0.9967, which is suggesting that the SFO kinetic model is applicable for this research. The slope of the straight line from equation 3 is k1/2.303 , where the value of the SFO rate (k1) was found to be 0.0055272 1/min.
PSO model is usually applied for chemisorption kinetics sorption of liquid solutions [25], the model is in equation 4 and its linear form is as in equation 5:
The plot of t/q against t for PSO model as in equation 5, didn’t yield straight line for the whole experimental data or even for any of its portions on contrary to the straight line of plot ln (qe-qt) against t for PFO model, which covers the whole experimental data and suggesting that the adsorption rate here is following PFO model which would be applied to calculate adsorption rate constant (k1).
Equation 6 is the intraparticle diffusion equation [26],
Where:
qt: Amount of adsorbate absorbed at any time, mg g−1
kp: Intraparticle diffusion rate constant, mg g−1 min−1/2
t: Time, min
c: Intercept, mg g−1
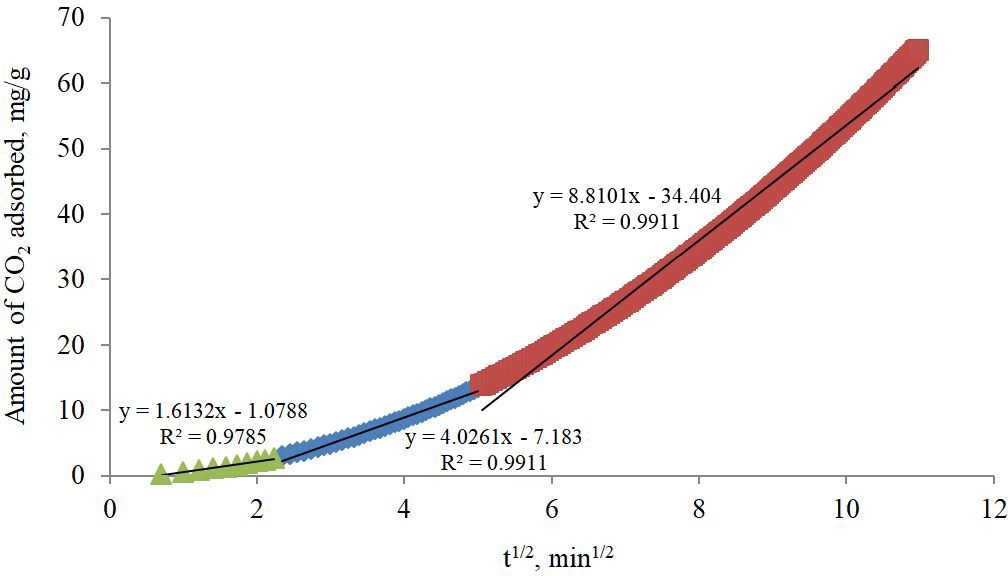
The multilinearity displayed in Figure 2, the plot of the amount of CO2 adsorbed (qt) against the square root of time (t1/2) is suggesting that more than one step is taking place. The straight line fitting the curve is not passing through the origin, indicating that the intraparticle diffusion is not the adsorption rate restrictive step [27]. The curve is divided into three zones where the slope of the linear part indicating the rate of adsorption and the rate controlling step is represented by the linear section with lowest slope value [28]. The first zone is the initial zone where the external diffusion of CO2 molecules through the bulk gas phase is taking place and the slope which is representing the adsorption rate is low. The second zone is the film diffusion where the mass transfer of CO2 molecules is continuing through the CO2 film surrounding the AC particles. The slope of the straight line of the second zone is higher than that of the initial zone but lower than that of the third zone due to the resistance exerted by CO2 gas film, which is indicating that this step combining with the initial zone step are slow and the overall adsorption rate is controlled by mass transfer and film resistances respectively. In the third zone, where the amount of CO2 molecules adsorbed (qt) versust 1/2 is displaying a straight line with high slope value indicating that CO2 molecules intraparticle diffusion step is fast, where CO2 molecules adsorption is enhanced by the fast CO2 -MEA reaction. The intercept (c) is an indicator of the thickness of the boundary layer surrounding the MEA-impregnated AC particles. Higher values of intercept suggest that the boundary layer is building up as the value of the c in the initial zone is less than that of zone 1, which is in turn less than that of zone 2 deducing that diffusion through the gas film may be considered as the controlling step [29]. CO2 adsorption in zone 2 is approaching its final stage and the active sites on MEA-impregnated AC particles are not able to adsorb more CO2 molecules.
Gas film diffusion model:The transportation of CO2 molecules from the gas stream bulk to the surface of the AC particles is playing a major role as the analysis of the intraparticle model showed that the mass transfer of CO2 molecules through the gas film is the limiting step of CO2 adsorption. To further inspect that gas film is the limiting step in CO2 molecules adsorption, gas film diffusion model was applied [30-32]:
The linearized form of equation 7 is as in equation 8:
Where,
F: Fractional adsorption equilibrium (F = qt /qe)
kfd: Film diffusion coefficient, min−1
t: Time, min
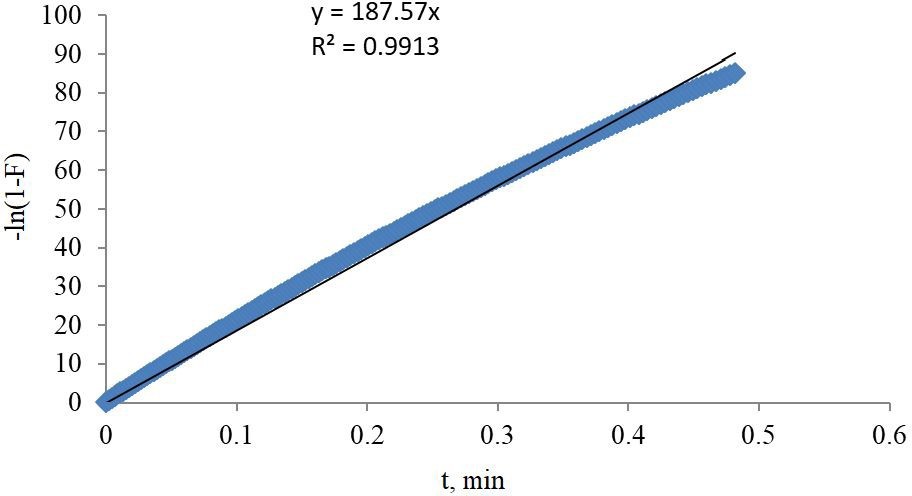
A plot as in Figure 3 of −ln (1 − F) vs t with intercept equal to zero and R2 equal to 0.99 is suggesting that adsorption kinetics is controlled by diffusion through the CO2 gas film surrounding the AC particles.
Avrami (JMAK) model:Johnson-Mehl-Avrami-Kolmogorov (JMKA) model, which is called Avrami model too, is expressed in equation 9, [32,33]. Avrami equation describes the growth of crystallites with respect to time. In this work Avrami equation is describing the increasing numbers of CO2 molecules by adsorption inside the AC pores.
Where, α is adsorption fraction at time t, kAv is the Avrami kinetic constant, and n is a constant which represents the mechanism of particles adsorption (growth).
The linearized form is as in equation 10:
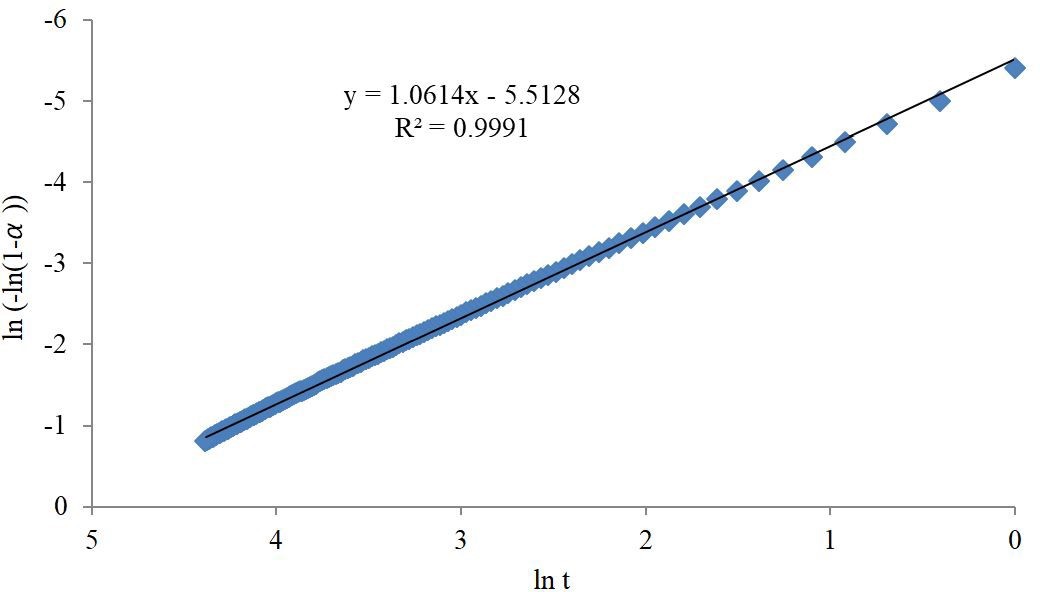
Plotting ln (-ln (1- α)) against ln t as in Figure 4 producing straight line (R2=0.9991) with intercept equal to nlnkAv and slope equal to n. Furthermore the value of Avrami exponent n, which is 1≤ n ≤ 2 suggesting one dimensional growth of crystallites and that the growth is homogenous [34], which is agreeing with exponent n in micropore filling method of Dubinin-Astakhov (D-A), equation 11 and its linearized form equation 13. D-A equation is applicable for homogeneous carbonaceous adsorbents with micropore structures [35]. It was found in other study [36] that the value of D-A exponent n for MEA-impregnated beds is showing less heterogeneity and more homogeneity with their exponent n value equal to 2, where the value of exponent n in AC is 3 - 1.5. Moving from 3 to 1.5 the microporous system would be getting more heterogeneous [37,38].
Where A is the adsorption potential given in equation 12:
And the linearized form of equation 10 is as in equation 13:
Adsorption of CO2 molecules from feed gas stream containing 15 % CO2 and 85 % N2 was performed in fixed bed packed column of non-impregnated and MEA-impregnated AC beds. Breakthrough time was employed as real time tool to evaluate the efficiency of the adsorption beds. CO2 monitor was used to display the concentration (%) of the gas stream exiting the adsorption column. Graphs of CO2 molecules concentration leaving the adsorption column plotted against time were obtained from the data acquisition logger connected to the outlet of the adsorption column.
Mathematical modeling of MEA-impregnated 500 µm adsorption bed:To formulate a general mathematical model corresponding to the mainly micropore adsorption mechanism and to cover the two stages mentioned earlier, the following assumptions were made:
1. The system operates under isothermal, isobaric and diabatic conditions.
2. The porosity of the adsorption bed was uniform and constant.
3. The equilibrium of adsorption is a nonlinear isotherm.
4. The velocity distribution is constant across the column diameter.
5. The volumetric flow rate is constant along the column.
Summarizes of the experimental parameters and simulation boundary conditions for the mathematical model validation are in
Table 1:
Mathematical model of MEA-impregnated AC bed:The mathematical model was based on the CO2 molecules breaking through the adsorption bed.
The adsorption of CO2 molecules was declining and more CO2 molecules were exiting the bed.
The general equation of mass balance with first order chemical reaction for CO2 in the feed gas:
Accumulation = Input – Output + Generation
As the mass balance would be conducted on CO2 molecules exiting the adsorption bed, the mass balance equation would be:
Output = Input – Accumulation + Generation
Where:
K1: Pseudo first order reaction constant, 1/min
Ci: Concentration of CO2 entering the AC bed, mol/ml
Co: Concentration of CO2 exiting the AC bed, mol/ml
Cacc: Concentration of CO2 accumulated in the AC bed, mol/ml
Equation 14 is an ordinary first order linear differential equation and the final solution would be as in Equation 15.
Initial boundary condition:
At t = 0, C = 0
n = -Ci
Then equation 15 would be:
Rearranging equation 16
The simulated results were validated by using the experimental results of the MEA-impregnated activated carbon bed. The simulated results were compared with the experimental data. The simulated data demonstrated a reasonable agreement with the experimental data, as the root mean square error (RMSE) calculated was 6.75915E-06. The simulated and experimental data of MEA-impregnated AC beds were plotted in Figure 5.
MEA-impregnated AC particles were used to adsorb CO2 from gas mixture. Results are showing that AC particles impregnated with MEA adsorb CO2 molecules in a pseudo first order reaction manner and that the controlling step in this reaction is the mass transfer of CO2 molecules from through the CO2 gas film and not the intraparticle diffusion of CO2 molecules inside the pores of MEA-impregnated AC particles. Due to the homogeneity of the MEA-impregnated activated carbon particles the adsorption of CO2 molecules follows the Avrami model of homogenous crystallites growth. The mass balance mathematical model showed that the experimental and simulated breakthrough curves have good agreement, as the root mean square error (RMSE) was 5.7678E-09. and 3.88532E-09 for non-impregnated and MEA-impregnated beds respectively, which also proved that the adsorption mechanism of both beds is the same.
The authors would like to thank University of Malay for offering the necessary fund for this research through the, University of Malaya Research grant UMRG RP15/2012A.
 |
| Figure 1: Plot of ln (qe-qt) against time |
 |
| Figure 2: CO2 Amount adsorbed, mg/g against square root of time, min1/2 |
 |
| Figure 3: Plot of -ln (F-1) against time |
 |
| Figure 4: Plot of ln (-ln (1- a)) against ln (t) |
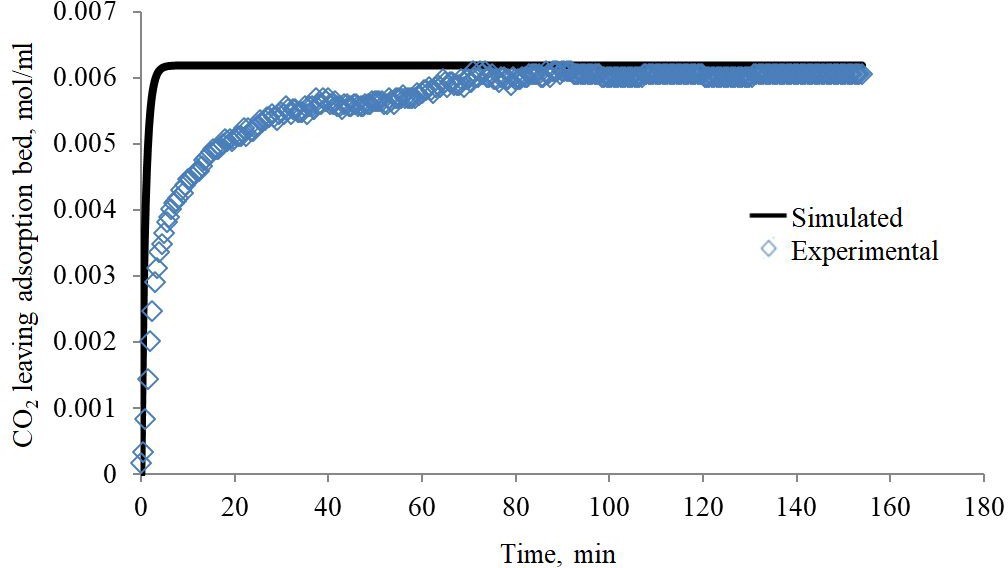 |
| Figure 5: Comparison of CO2 experimental and simulated breakthrough curves for MEA-impregnated AC bed (Sampled at column outlet) |
Operating conditions |
|
|
Pressure |
1 atm |
|
Temperature |
25 oC |
|
Inlet concentration |
6.05118E10-6 mol/ml |
|
Inlet volumetric flow rate |
10 ml/min |
|
Adsorption column |
|
|
Material |
Glass |
|
Inside diameter |
1 cm |
|
Bed height |
9 cm |
|
Bed weight |
5 g |
|
Bed Volume |
7.23 cm3 |
|
Adsorbent properties |
|
|
Bed type |
Non-impregnated AC |
MEA-impregnated AC |
Particles size |
500 µm |
500 µm |
Micropore surface area |
675 m2/g |
65 m2/g |
Micropore particle porosity |
0.0956 cm3/g |
0.020 cm3/g |
Porosity |
0.684 |
0.620 |
Bulk density |
1.6387 cm3/g |
1.6228 cm3/g |
Bed Volume |
7.2285 cm3 |
6.2857 cm3 |
Pseudo 1st order reaction constant (k) |
- |
0.004836 1/min |






































