Price Transmission and Signal of Cowpea across Zones and Value Chain in Niger State of Nigeria

This study investigated price transmission and signals of the three major urban cowpea markets and their respective adjunct rural market across the zones and value chain in Niger state of Nigeria using monthly time series data spanning from January 2003 to December 2016. The selected urban markets were Bida, Minna and Kontagora, and their adjunct markets were Lafene, Zungeru and Manigi, respectively. Model build on the assumption of linear and symmetric price transmission was used to analyze the data. The stationarity tests showed that the price series of all the variables were integrated of order one. The cointegration test results of the markets both at horizontal and vertical integrated levels proved that despite that these markets were spatially separated geographically; they were well connected in terms of price transmission across them. It was observed that price changes are temporary and would converge to an equilibrium within a given time span. However, Bida market was found to me more pricing and operational efficient when compared to its counterparts because of its close proximity to the largest terminal markets for cowpea in the country i.e Lagos state and other states in the southwest of Nigeria. Furthermore, the price signals across the zones and value chain will be well transmitted, indicating that price changes in one zone are consistently related to the price changes in other zones and are able to influence the prices in other zones. However, the direction and intensity of price changes may be affected by the dynamic linkages between the demand and supply of cowpea. A proper focus on domestic supply management along with international trade coupled with strong market surveillance and intelligence efforts would help control escalating prices and also help in minimizing the distortions widening the gap between the wholesale and retail prices of cowpea.

Keywords: Price Transmission; Signals; Across Zones; Value Chain; Cowpea Markets; Nigeria

The rapid development in agricultural research and the introduction of technological innovations viz., high-yielding varieties, improved agricultural implements, fertilizers and pesticides, have brought about a breakthrough in Nigeria agriculture. This development in the agriculture, popularly known as the green revolutions, has given rise to new problems in agricultural marketing. It is essential to maintain the tempo of these revolutions. The farmers should be assured of a fair price for their produce, failing which they may lose the incentive to increase agricultural production. A fair price for the produce may be assured when there is an orderly marketing system in the country. Market intelligence being an important adjunct of orderly marketing has emerged as another problem. With the increased marketed surplus and opening up of the trade, the importance of market intelligence has increased. Farmers market their produce in the villages and nearby assembling centers out of their ignorance of the prevailing price in the nearby primary wholesale, secondary wholesale and terminal markets. Traders take the full advantage of the ignorance of the farmer because they have full knowledge of the prices prevailing in other markets, thus, placing these traders in a superior bargaining position. But an orderly marketing system can be created only when the problems, which have emerged, are effectively tackled. There is an urgent need in the present context for tackling the emerging problems of agricultural marketing more resolutely and efficiently than before. The improvement in the domestic marketing system has assumed special significance with the launch of green alternative in 2016 and opening up of the external trade regime.

The study made use of monthly time series data spanning from January 2003 to December 2016 of one major urban cowpea market with its respective one major adjunct rural market in each of the three zones cutting across the state. The chosen urban adjunct rural (urban – rural) markets were Bida-Lafene, Minna–Zungeru and Kontagora–Manigi. The data source is Niger State Bureau of Statistics (NIBS). The analytical tools used are given below:

The Augmented Dickey-Fuller test (ADF) is the test for the unit root in a time series sample (Blay et al., 2015) [1]. The autoregressive formulation of the ADF test with a trend term is given below:

Where, pit is the price in market i at the time t, ∆pit (pit – pt-1) and α is the intercept or trend term.

The Johansen procedure is a multivariate generalization of the Dickey-Fuller test and the formulation is as follows (Johansen,1988):

So that

Where, pt and are (n×1) vectors; At is an (n x n) matrix of parameters; I is an (n x n) identity matrix, and ∏ is the (A1-1) matrix.

Using the estimates of the characteristic roots, the tests for the number of characteristic roots that are insignificantly different from unity were conducted using the following statistics:

Where, λi denotes the estimated values of the characteristic roots (eigen values) obtained from the estimated ∏ matrix, and T is the number of usable observations.

Granger (1969) causality test was used to determine the order and direction of short-term and long-term equilibrium relationships. Whether market p1 Granger causes market p2 or vice-versa was checked using the following model [2]:

A simple test of the joint significance of was used to check the Granger causality, i.e

The VECM explains the difference in y_t and y_t-1(i.e.∆y_t) it is shown below (Sadiq et al., 2016a; Sadiq et al., 2016b) [3,4]:

It includes the lagged differences in both x and y, which have a more immediate impact on the value of ∆y_t

The GIRF in the case of an arbitrary current shock, δ , and history, is specified below (Rahman and Shahbaz, 2013; Beag and Singla, 2014)[5,6]:

For measuring the accuracy in fitted time series model, mean absolute prediction error (MAPE), relative mean square prediction error (RMSPE) and relative mean absolute prediction error (RMAPE) (Paul, 2014) and R2 were computed using the following formulae [7]:

Where, R²= coefficient of multiple determination, A_t= Actual value; F_t = Future value, and T = time period(s)

Too many lags could increase the error in the forecasts; too few could leave out relevant information. Experience, knowledge and theory are usually the best way to determine the number of lags needed. The following information criteria most widely used viz. Akaike information criterion (AIC), Schwarz Bayesian information criterion (BIC) and Hannan-Quinn criterion (HQC) were used to select the optimal truncation lag length to ensure that the errors are white noise in ADF. Based on democratic principle, the test results as shown in Table 1 reveal that the optimum lag length appropriate for the specified variables is lag one (1) because all the information criteria chose lag one (1) as indicated by the asterisks of the information criteria. This means that in generating ADF and all the subsequent models, the optimum lag length of time series should be 1 in order to obtain more interpretable parsimonious results and avoid biasness of time series due to their sensitive nature towards lag length.

The stationarity of the price indices was tested before establishing the causal relationship between different markets in the state. The Augmented Dickey Fuller (ADF) test was employed and the presence of unit root was checked under different scenarios of the equation such as with intercept, with intercept and trend, and none (Table 2). ADF-GLS test, which provides an alternate method for correcting serial correlation and heteroscedasticity, was used to validate the results. The ADF results of the unit root test did not reject the null hypothesis of the presence of unit root for all the price series when the variables were considered at the level, as indicated by the t-statistic values which were greater than the t-critical values at 5% probability level. At the succeeding level, the first differenced series of all the price variables were found to be stationary, as indicated by the t-statistic values which were lower than the t-critical values at 5%probability level. Also, the ADF-GLS results of unit root test show that all the price series variables were non-stationary at level as indicated by t-statistic values which were higher than t-critical at 5% probability level; but at first difference, they became stationary as shown by t-statistic values which were lower than t-critical at 5% probability level, thus, validating robustness of the earlier results generated using ADF-test. Since the variables were non-stationary at levels, any attempts to use them will lead to spurious/nonsense regression and this is not ideal for policy making and cannot be used for long run prediction. With the evidence that the price series were non-stationary and integrated of order one I (1), the test for cointegration among the selected cowpea markets in the state using Johansen’s maximum likelihood approach was applied.

The results of the horizontal cointegration tests for the rural and urban markets are presented in (Table 3).Using the identified optimal lag length i.e lag 1, the Johansen co-integration test was undertaken and the co-integrating equation was identified using the trace statistic and max eigen value test. For rural markets, the cointegration tests showed only two co-integrating equations as evidenced by the trace and maximum eigen-values which were below their corresponding critical values at 5% significance level, indicating that there is one stochastic trend present in the system. Also, the cointegration tests showed only two co-integration equations for the selected urban markets for cowpea in the state as indicated by the trace and maximum eigen-values which were below their corresponding critical values at 5% significance level, indicating that they shared the same stochastic trend in the system. In summary, it means that across the rural and urban markets of cowpea in the different region of the state, there was two cointegrating relationship. Since both tests across the rural and urban markets for cowpea confirmed that all the three selected markets under each scenario had 2 cointegrating vectors out of 3 cointegrating equations, it implies that in each scenario, the markets were well integrated and price signals were transmitted from one market to the other to ensure efficiency. The higher the number of co-integrating vectors the stronger the relationship between the variables in the system. Thus, Johnson cointegration test has shown that even though the cowpea markets under each case in the state are geographically isolated and spatially segmented, they were well-connected in terms of cowpea prices, demonstrating that the markets under each scenario had long-run price linkage across them. Since these markets in each scenario i.e producer and wholesale markets move together, in the long-run, they are likely to establish long-run equilibrium.

The results of a horizontal pair-wise cointegration that was also performed across the rural and urban markets are given in (Table 4). The decomposition analysis across the rural and urban markets is as follow: For the rural markets, the test showed that each market pair viz. Lefane-Zungeru, Lefane-Manigi and Zungeru-Manigi had one cointegrating equation, meaning that these market pairs were cointegrated and there exists long-run price association between them. For the urban markets, the test showed each market pair viz. Bida-Minna, Bida-Kontagora and Minna-Kontagora, had one cointegrating equation, indicating that these market pairs were cointegrated and there exists long-run price movement between them. However, a situation of no cointegration between market pair across the rural and urban market was not observed, thus, indicating that in pair-wise the power of these markets was not concentrated in the hand of few; there was an adequate flow of market information and proper marketing infrastructure.

In addition to the horizontal cointegration, the vertical cointegration between the rural and urban price of cowpea for different markets in the state were also investigated using Johansen’s cointegration test (Table 5). The tests showed that each market pair viz. Bida-Lefane, Minna-Zungeru and Kontagora-Manigi had one cointegrating relationship, indicating that these market pairs were vertically integrated markets were cointegarted. Therefore, it can be inferred that despite been spatially separated, there existed price transmission between these market pairs in the long-run i.e they had long-run price association or co-move together in the long run, and thus, likely to establish equilibrium in the long-run.

The results of the VECM estimates for the multivariate horizontal cointegrated prices of selected rural markets in the different regions of the state are presented in (Table 6). The coefficient of the error correction term for Lafene and Manigi markets were significant for all the three combinations, confirming the presence of partial horizontal cointegration. The coefficient of the error correction term was negative and significant in the case of the Lafene market; and, positive and significant for the Manigi market. This implies that the prices of cowpea in these markets were stable in the long-run and any deviation in these due to external shocks that occur in the short-run, where well adjusted. However, the error correction term of prices in Zungeru market was positive but non-significant; indicating that this market did not correct its previous period error if there is any shock originating from any of the short-run equilibrium. This outcome is not surprising because the quantity of arrival in this market is low when compared to the quantity of arrivals in the two selected markets.

The error correct term coefficients for Lafene and Manigi market prices were -0.465 and 0.346, indicating how fast the dependent variables absorb and adjust themselves for the previous period disequilibrium errors. In other words, the VEC coefficient measures the ability of Lafene and Manigi market prices to incorporate shocks or speculations in the prices. In this case, Lafene and Manigi markets absorbed 45.6% and 34.6%, respectively to move towards equilibrium in the prices. The information flow was more pronounced in the Lafene market as evident from the magnitude of the VEC coefficient, and also because it is a pure satellite of Bida market. A clear unidirectional lead-lag relationship can be established that flows from Lafene market to Zungeru-Manigi markets.

The presence of co-integration indicates the existence of long-run equilibrium among the cointegrated variables. The long-run and short-run dynamics of the cointegrated equation was modeled through the vector error correction model (Table 7). The estimates of vector error correction model show that only prices of Bida market speed of adjustment coefficient was negative and significant, implying that prices in this market tend to converge in the long-run; while the speed of adjustment coefficients for Minna and Kontagora market prices were positive and significant, indicating that they diverge from the equilibrium. For Bida market the speed of adjustment coefficient was -0.464, indicating that 46.4% of divergence from the long-run equilibrium was been corrected each month, i.e it will take about 16 days to re-establish equilibrium if there is distortion from any of the short run equilibrium. In the case of Minna and Kontagora market prices, the speed of adjustment coefficients were 0.399 and 0.30 respectively, implying that 39.9% and 30% of divergence from the long-run equilibrium were been corrected each month, i.e it will take about 18 and 21 days to re-establish equilibrium for Minna and Kontagora market prices respectively, if there is distortion from any of the short run equilibrium. The prices of cowpea in Bida market is above the equilibrium and quickly falls back towards the price level of MinnaKontagora markets, while that of Minna and Konatgora markets where below the equilibrium and quickly adjusts towards the price levels of Bida-Kontagora markets, and Bida-Minna markets, respectively. The process of adjustment, however, was relatively faster between the markets of Bida to Minna-Kontagora; and, Minna to Bida-Kontagora. This might be due to lesser transfer and transaction costs in these markets due to proximity and better infrastructure. In addition, the Bida market gets its product cleared off immediately because of its proximity to largest consuming markets-south western part of Nigeria, while Minna market is situated in the metropolitan area which enhances its efficiency. Furthermore, based on the sign of the error correction term, Bida market is efficient in pricing because of its market size-large quantity of arrivals; in terms of establishment it is an older market; the market power is concentrated in the hand of many traders, and the traders have adequate access to information. In the case of Minna and Kontagora despite been an old establishment, large markets and having adequate access to market information, the major factor hindering its efficiency is that the power of these markets is concentrated in the hand of few traders.

The acceptance of cointegration between two variables indicates that there they are likely to establish long-run equilibrium between them and this means that vector error-correction model (VECM) is applicable, which combines the long-run relationship with the short-run dynamics of the model. The bivariate VECMs of cowpea prices for the horizontal rural markets in different regions in the state are shown in (Table 8). A perusal of the results shows that the prices of market pair viz. Lefane-Zungeru did not establish long-run equilibrium as evidenced by the ECT coefficient which was not significant, but in the reverse situation, the prices of the market pair: Zungeru-Lafene established long-run equilibrium as evidence by the ECT which is significant. Also, Lefane-Manigi market pair established long-run equilibrium, likewise Manigi-Lefane market pair established long-run equilibrium as evidence by the ECT coefficients which were significant. For Zungeru-Manigi market pair there exist long-run equilibrium, likewise ManigiZungeru markets there exist long-run equilibrium as indicated by the ECT coefficients which were significant. In other words, for Lefane-Zungeru markets there was no long-run causality running from Zungeru market to Lefane market but there was longrun causality running from Lefane market to Zungeru market indicating that approximately 235% of long run disequilibrium is corrected each month by changes in the prices of cowpea at Lefane market; for Lefane-Manigi markets, there was long-run causality running from Manigi market to Lefane market indicating that about 41.5% of long run disequilibrium is corrected each month by changes in the prices of cowpea at Manigi market, likewise a long-run causality running from Lefane market to Manigi market indicating that approximately 38.4% of long run disequilibrium is corrected each month by changes in the prices of cowpea at Lefane market; and, for Zungeru-Manigi markets, there was long-run causality running from Manigi market to Zungeru market indicating that approximately 56% of long run disequilibrium is corrected each month by changes in the prices of cowpea at Manigi market, likewise a long-run causality running from Zungeru market to Manigi market indicating that approximately 3.6% of long-run disequilibrium is corrected each month by changes in the prices of cowpea at Zungeru market.

The acceptance of cointegration between two series implies that there exists a long-run relationship between them and this means that vector error-correction model (VECM) is applicable, which combines the long-run relationship with the short-run dynamics of the model.

Therefore, after confirming cointegration in prices of cowpea across different urban and rural markets in the state, the error correction terms (ECT) were measured and are reported in (Table 9). In the case of urban markets, all the pair-wise market VECM established equilibrium as evidenced by the error correction terms which were significant at various probability levels. The ECT coefficients for Bida-Minna markets were -0.061 and 0.672, respectively, indicating that prices of cowpea in Bida market is too high and it quickly falls back towards the price level of Minna market at the speed of 6.1% which is very low, while the prices at Minna market quickly adjust back towards the price level of Bida market at the same time that the Bida market prices are adjusting. For Bida-Kontagora markets, the ECT coefficients are -0.44 and 0.32, respectively, meaning that prices of cowpea in Bida market is too high and it quickly falls back towards the price level of Kontagora market at the speed of 44% which is high, while the prices at Kontagora market quickly adjust back towards the price level of Bida market at the same time that the Bida market prices are adjusting. Also, in the case of cowpea prices for Minna-Kontagora markets, the ECT coefficients are -0.88 and 0.056, respectively, implying that the prices of cowpea in Minna market is too high and it quickly falls back towards the price level of Kontagora market at the speed of 88% which is very high, while the prices at Kontagora market quickly adjust back towards the price level of Minna market at the same time that the Minna market prices are adjusting. The time frame at which cowpea prices at Bida market re-established equilibrium with Minna and Kontagora were 28 and 17 days, respectively; time frame at which prices at Minna market re-established equilibrium with Bida and Kontagora markets were 10 and 4days, respectively; and, the time frame at which Kontagora market re-established equilibrium with Bida and Minna markets were 20 and 28 days, respectively. Based on these findings it can be inferred that Bida market is more established than Minna and Kontagora markets, and in turn, Minna market is more established than Kontagora market. Furthermore, a clear unidirectional lead lag-relationship can be established that flows from Bida market to Minna market, and Bida market to Kontagora market. This justified the earlier results which proved that Bida market is more technical and pricing efficient when compared to the other two selected markets in different regions of the state.

The results of bivariate VECMs for vertically integrated cowpea markets in the state are presented in (Table 10). A cursory review shows that the ECT coefficients for Bida-Lefane vertical market integration were -0.72 and 0.30, respectively, and all significant, indicating that the prices of cowpea at Bida market (urban) converge towards its long-run equilibrium at a high-fast speed while the prices of cowpea at Lefane market (rural) converge towards its long-run equilibrium at a low speed. The ECT coefficients for Minna-Zungeru vertical market integration were -0.725 and 0.983, respectively, and all significant, indicating that the prices of cowpea at Minna market (urban) converge towards its long-run equilibrium at a high-fast speed while the prices of cowpea at market Zungeru (rural) converge towards its long-run equilibrium at a very high-fast speed. Also, The ECT coefficients for Kontagora-Manigi vertical market integration were -0.491 and 0.238, respectively, and were all significant, indicating that the prices of cowpea at Konatgora market (urban) converge towards its long-run equilibrium at a moderately-fast speed while the prices of cowpea at Manigi market (rural) converge towards its long-run equilibrium at a very low speed. Furthermore, on the basis of sign of the ECT coefficient, it was observed that the prices of cowpea in all the selected urban (supply) markets were high and above the equilibrium, while that of all the selected rural (producing) markets were low and below the equilibrium, thus, signifying that all the urban markets were more efficient than the rural markets which are attributed to adequate information, proper infrastructure and are well-established institution considering the years existence of these markets. Based on these findings, a clear unidirectional lead-lag relationship can be established that flows from urban (supply) markets to rural (producing) markets i.e the prices of cowpea in urban (supply) markets had lead effects on prices of cowpea in their respective annexed rural (producing) markets.

Having established the existence of co-integration between the producer prices of rural markets, the Granger causality test was used to identify the causal variable between them. The results of pair-wise Granger causality test in Table 11 showed that there was bidirectional influence of prices between Lefane and Manigi markets, implying that both markets exhibit feed forward and feed backward mechanism in price formation between them. The results of pair wise granger causality for Zungeru-Manigi market pair shows that the Zungeru market exhibited strong exogeniety with Manigi market (unidirectional causality), i.e Zungeru market had a causal effect on price formation in the Manigi market, while prices in the Manigi market in-turn did not exert influence on price formation in the Zungeru market. Thus, the price of cowpea in the Zungeru market seemed to be exogenous and was determined outside the system perhaps by quality, bad news, and to some extent by export demand. Furthermore, it was observed that LefaneZungeru market pair had no causal effects on each other i.e neither the former granger cause price formation in the latter nor the latter granger cause price formation in the former. Therefore, based on these outcomes it can be inferred that there was super exogeneity between the prices of cowpea in Lefane-Zungeru market pair, strong exogeneity between prices of cowpea in ZungeruManigi market pair, and strong endogeneity between Lefane-Manigi market pair. In addition, since Lefane-Manigi markets were satellite of each other in price formation, and Manigi market again is a pure satellite of Zungeru market in price formation, while Zungeru market is not a satellite to any of the selected rural markets, thus, it implies that prices of cowpea in Zungeru market has direct and indirect influence on the rest of the selected rural markets in different regions of the state.

After establishing cointegration among different urban cowpea markets, granger causality was also estimated between the selected pairs of urban cowpea markets in the state. The granger causality shows the direction of price formation between two markets and related spatial arbitrage, i.e., physical movement of the commodity to adjust the prices difference. The results of granger causality tests presented in Table 12 reveals that all the two X² for the causality tests of supply prices in Bida market on other markets were statistically significant. Thus, the null hypothesis of no granger causality was rejected in each case for Bida market. Besides, Minna and Kontagora markets in each had one X² statistically significant on other market prices. According to the granger causality test, there were bidirectional causalities between the Bida-Minna and Bida-Kontagora supply markets, implying that the former market in each pair granger causes the supply price formation in the latter market which in turn provides the feedback to the former market as well. The presence of the bi-directional Granger Causality between these urban (supply) markets indicates that there is a perfect price transmission mechanism between these market pairs.

Further, market pair viz. Minna-Kontagora, has no direct causality between them, indicating that neither Minna market granger causes the price formation in Kontagora market, nor the Kontagora market granger causes the price formation in Minna market. In other words, there is no long-run price association between these market pair. Therefore, it can be inferred that supply prices in Bida market have lead influence/effect on the other selected urban markets, thus, justifying the earlier finding which proved Bida market to be more developed in terms of establishment; have higher quantity of arrival which get cleared within shortest possible due to its proximity to the largest terminal and export market (south-west of Nigeria); the market power concentration is in the hand of many traders, and there are adequate flow of information which minimizes arbitrage in the market. In addition, the result implies a perfectly competitive market situation and strong endogeneity between supply prices of Bida markets and the supply prices of other selected urban markets in other regions in the state.

The results of variance decomposition for the selected urban markets against its component, like-wise the selected rural markets against its component are presented in (Table 14). The decomposition detailed for the selected urban markets are as follow: For Bida market, in the short-run (first quarter), a shock to price of cowpea in Bida market will account 84.48, 1.90 and 13.62% variations of fluctuation in prices at Bida (own shock), Minna and Kontagora markets, respectively; while in the long-run (last quarter), a shock to price in Bida market will account for 71.53, 2.43 and 26.03% variation of fluctuation in prices at Bida (own shock), Minna and Kontagora markets, respectively. In the case of Minna market, in the short-run, an impulse to price of cowpea in Minna market can cause 9.93, 87.55 and 2.52% of variation in the fluctuation of prices in Bida, Minna (own shock) and Kontagora markets, respectively; while in the long-run (last quarter), an impulse to price in Minna market can cause 30.83, 56.41 and 12.76% of variation in the fluctuation of prices in Bida, Minna (own shock) and Kontagora markets, respectively. Also, in the case of Kontagora market, in the short-run (first quarter), an innovation to the price in Kontagora market can cause 47.48, 1.25 and 51.28% of variation in the fluctuation of prices in Bida, Minna and Kontagora (own shock), respectively; while in the longrun (last quarter), an innovation to price in Kontagora market can cause 61.35, 2.23 and 36.43% of variation in the fluctuation of prices at Bida, Minna and Kontagora (own shock), respectively. For horizontal integrated rural markets: a shock to price of cowpea in Lefane market in the short-run (1st quarter) can cause 84.96, 0.74 and 14.30% of variation in the fluctuation of prices in its own market, Zungeru and Manigi markets, respectively; while in the long-run (last quarter) it can cause 73.37, 1.33 and 25.30% variation in the fluctuation of prices in its own market, Zungeru and Manigi markets, respectively. A shock to price in Zungeru market in the short-run (1st quarter) will cause 37.83, 54.77 and 7.40% of variation in the fluctuation of prices in Lefane market, its own market (Zungeru) and Manigi market, respectively; while in the long-run (last quarter) it will cause 56.39, 23.30 and 20.31% of variation in the fluctuation of prices in Lefane, Zungeru (own shock) and Manigi markets, respectively. Also, an impulse on price in Manigi market in the short-run (1st quarter) can cause 47.75, 0.51 and 51.74% of variation in the fluctuation of prices in Lefane, Zungeru and Manigi (own shock) markets, respectively; while an impulse in the long-run can cause 63.19, 1.24 and 35.58% of variation in the fluctuation of prices in Lefane, Zungeru and Manigi (own shock) markets, respectively. Furthermore, results clearly show that the shock originating from a respective market at both time periods is more pronounce on the respective market itself when compared to its effect on other markets.

Table 15 shows the result of variance decomposition for the vertically integrated cowpea markets in the state. A cursory review of the results for Bida-Lafene market pair show that a shock to the price in Bida market in the short-run (1st quarter) can cause 84.20 and 15.80% of variation in the fluctuation of prices on its own market and Lefane market; respectively; while in the long-run (last quarter) it will cause 77.54 and 22.46% of variation in the fluctuation of prices in its own market and Lefane market, respectively. In the reverse situation, a shock to price in Lafene market in the short-run (1st quarter) can cause 67.01 and 32.99% of variation in the fluctuation of prices in Bida market and on its own market, respectively; while in the long-run (last quarter) it will cause 73.03 and 26.97% of variation in fluctuation of prices in Bida and Lefane markets, respectively. For Minna-Zungeru market pair, an innovation to price in Minna market in the short-run (1st quarter) can cause 84.37 and 15.63% of variation in the fluctuation of prices in Minna and Zungeru markets, respectively; while in the long-run (last quarter) it can cause 50.46 and 49.54% of variation in the fluctuation of prices in Minna and Zungeru markets, respectively. While a shock to price in Zungeru market in the shortrun (1st quarter) can cause 9.88 and 90.12% of variation in the fluctuation of prices in Minna and Zungeru markets, respectively; while in the long-run (last quarter) it can cause 10.02 and 89.98% of variation in the fluctuation of prices in Minna and Zungeru markets, respectively. For Kontagora-Manigi market pair, a shock on Kontagrora market in the short-run (1st quarter) can cause 89.91 and 10.09% of variation in the fluctuation of prices in Kontagora and Manigi markets, respectively; while in the long-run it can cause 80.40 and 19.60% of variation in the fluctuation of prices in Kontagora and Manigi markets, respectively. A shock to price in Manigi market in the short-run (1st quarter) can cause 64.80 and 35.20% of variation in the fluctuation of prices in Kontagora and Manigi markets, respectively; while in the long-run (4th quarter) it can cause 73.68 and 26.33% of variation in the fluctuation of prices in Kontagora and Manigi markets, respectively.

The results of diagnostic statistics of VECM models for horizontal integrated and vertically integrated markets are presented in (Table 16). The autocorrelation test for each VECM model indicates that the residuals are not serially correlated as evidenced from the Ljung-Box Q-statistics which are not different from zero at 10% probability level (p>0.10), thus indicating no autocorrelation. The Arch tests for each VECM models revealed that there is no information transmission between the preceding and succeeding residuals as evidenced from the Lagrange multiplier (LM) test statistics which were not different from zero at 10% probability level (p>0.10), thus indicating no Arch effects are present. Also, the stability tests indicated that none of the models was misspecified as evidence from the eigen-values which shows that none of the remaining eigen-values appears close to the unit circle. Furthermore, the result of normality test for each VECM models indicated that the residuals are not normally distributed as evidence from Doornik-Hansen test X2 which is different from zero at 10% probability level (p< 0.10). However, when dealing with time series data, non-normality of the residuals is not considered a serious problem, because in most cases these data are not normally distributed. Therefore, based on the outcome of the diagnostic statistics, it can be inferred that all the results were valid as all the models used were the best fit.

The model verification is concerned with checking the residuals of the model to see if they contained any systematic pattern which still could be removed to improve the VECM. This was done viz. investigating the autocorrelations and partial autocorrelations of the residuals at various lags. Using the computed values, it was found that these autocorrelations were not significantly different from zero (Table 16a-b). These proved that the VECM model was an appropriate model for forecasting the data under study

One-step ahead forecast of price along with their corresponding standard errors using naïve approach for the period August 2016 to December 2016 (total 5 data points) in respect of the VECM fitted models was computed.

The forecasting ability of the VECM models of price series for the urban and rural markets were judged on the basis of mean absolute prediction error (MAPE), root mean square error (RMSE) and relative mean absolute prediction error (RMAPE) values (Table 17a). A perusal of Table 17b shows that for all the price series variables, RMAPE is less than 10 percent, indicating the accuracy of the VECM models used.

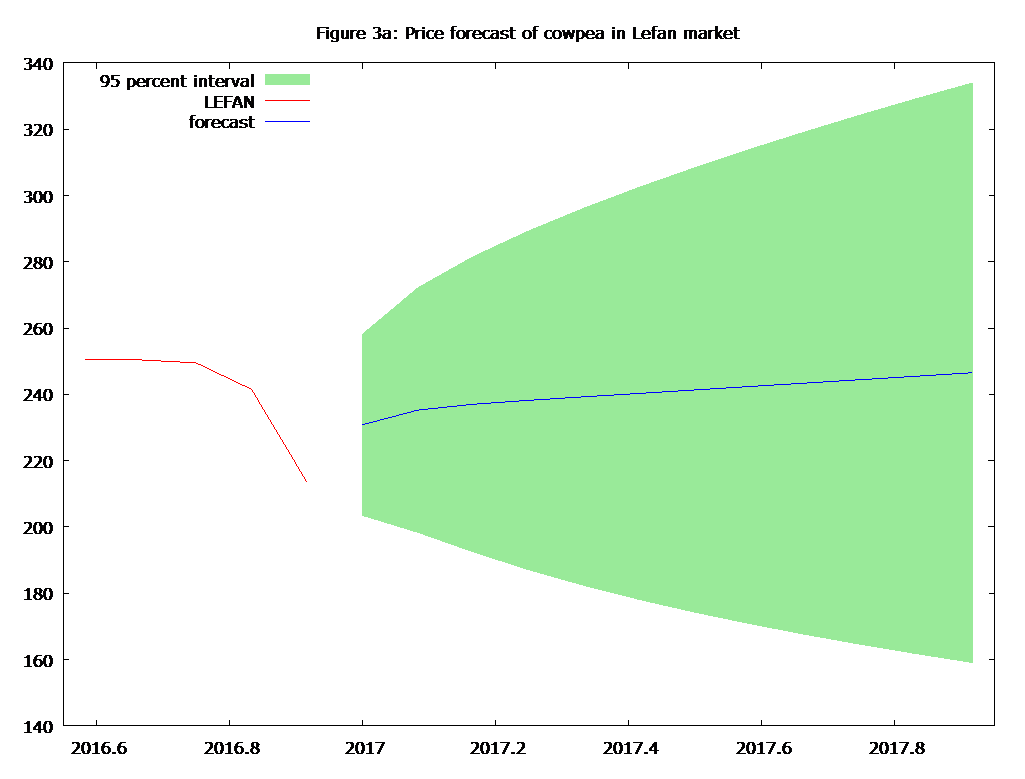
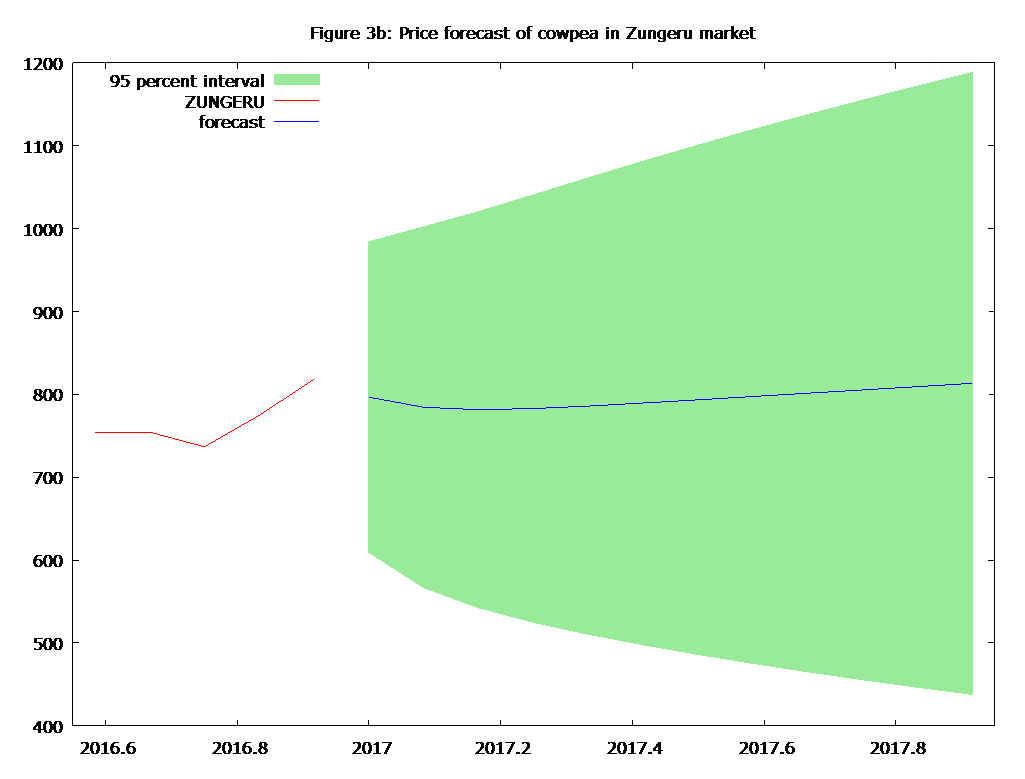
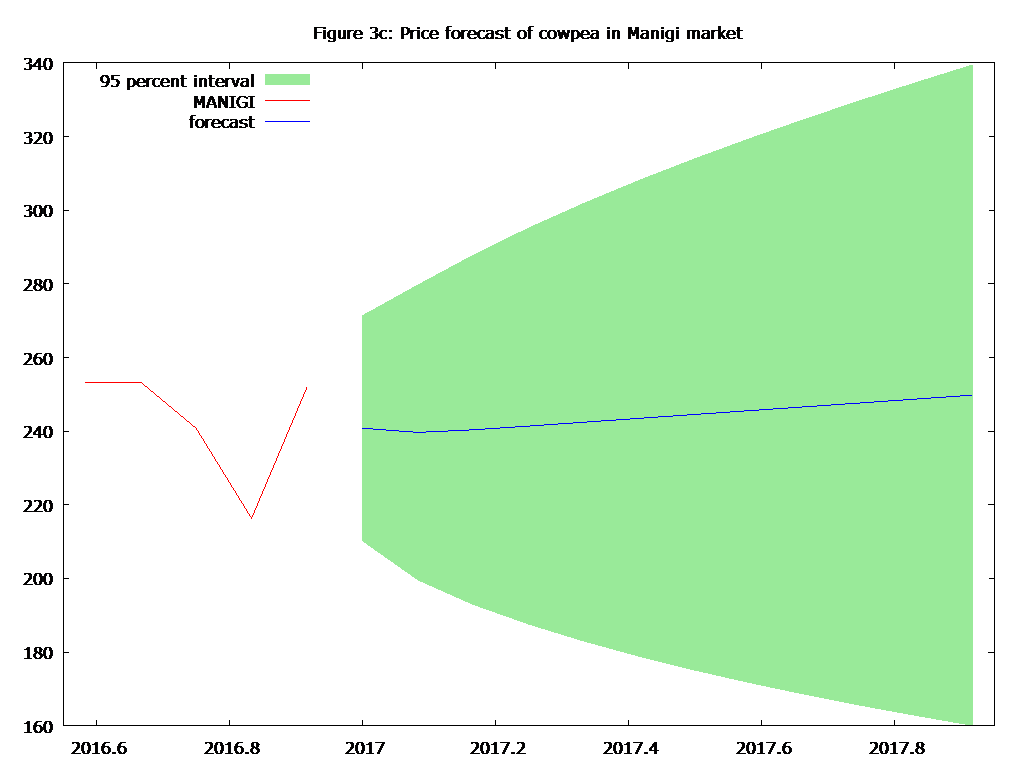
One step ahead out of sample forecast of cowpea price (N/Kg) for the urban and rural markets during the January 2017 to December 2017 have been computed. The actual data points are shown in Table 17c and also depicted in Figure 2-3 to visualize the performance of the fitted model. A cursory review shows that prices of cowpea in all the markets with the exception of Zungeru market will be marked by slight variation i.e will witness slight variation as evidenced by the standard error values. Further, in the situation of bad-news (inflation) the prices in each of the market would not exceed its respective price upper limit, and in the case of good-news (administered prices), the prices in each of the market would not go below its respective price lower limit. For policy implication, the government should put in place mechanism to checkmate virulent price instability that will occur in Zungeru market in order to protect itself and all market participants, even though this kind of measure will amount to the creation of imperfection in cowpea market in the state.

Note Row-wise: Figure 2a, 2b, 2c, 3a, 3b, 3c are price forecasts of cowpea in Bida, Minna, Kontagora, Lefane, Zungeru and Manigi markets, respectively

The present study focused on price transmission and signals of three major urban cowpea markets and their respective adjunct rural markets across the zones and value chain in Niger state of Nigeria. The results showed that the markets both at horizontal and vertical integration levels were integrated of order one, i.e at the level they were non-stationary, but at first difference they became stationary, thus, justifying the use of cointegration test. The cointegration test results of the markets both at horizontal and vertical integration levels proved that despite that these markets were spatially separated geographically they were well connected in terms of price transmission across them. Also, it was observed that almost all the error correction terms (ECTs) were statistically significant, meaning that the system once in disequilibrium tries to come back to the equilibrium situation. This coefficient (ECT), known as the attractor, helps absorb the effects of shocks and keeps prices in a long-term equilibrium relationship. The higher the attractor (in absolute value), the faster the speed of price adjustment towards its equilibrium level. Virtually under all scenarios, Bida market was found to be more price and operationally efficient that all the selected urban markets because of its close proximity to the largest terminal markets for cowpea in the country i.e Lagos state and other states in the southwest of Nigeria. Low pricing efficiency of cowpea in Minna market is associated with ‘bull raid’ activities of the traders, while the low pricing efficiency of Kontagrora market can be attributed to the dampening effects caused by the glut in the leading cowpea producing markets in the country which are located in the neighbouring states i.e Kebbi, Sokoto, Zamfara all in the North-western part of the country. However, the rates of adjustments for most of the markets were high when prices were influenced by the changes in each other’s price. Based on findings it can be inferred that the price signals are transmitted across zones and value chains, i.e price changes in one zone are consistently related to the price changes in other zones and are able to influence the prices in other zones. However, the direction and intensity of price changes may be affected by the dynamic linkages between the demand and supply of cowpea. The market outlook in terms of forecast and attendant volatility for all the markets except Zungeru markets looks bright and promising as indicated by their respective standard deviation values which were small. The insights from this study can be used to improve the information precision to predict the price movements used by marketing operators for their strategies. Also, the policy makers can use it to design suitable marketing strategies to bring more efficiency to the markets.