Bernoulli Equation in the Mitral Valve of Heart

Objective: The objective of this paper is to study and give an algorithm for the mechanisms of mitral valve of the heart based on mathematical techniques and Bernoulli’s equation.

Background:: The mechanics of the mitral valve leaflet as a nonlinear, inelastic and anisotropic soft tissue results from an integrated response of many mathematical/physical indexes’ that illustrate the tissue.

Methods and Results: Utilizing mathematical techniques and Bernoulli’s equation, we can make a geometrical modeling of the mitral valve leaflets and give available and valuable clinical benefit information of the Mitral valve behaviors for physician. Echocardiography was performed on healthy volunteers. Data evaluated included: velocity (radial, longitudinal, rotational and vector point), displacement (longitudinal and rotational), strain rate (longitudinal and circumferential) and strain (radial, longitudinal and circumferential) of all leaflet segments. Using these data, force vectors of myocardial samples and a new formula that was provided by Bernoulli equation, we were able to see what’s happening around the mitral valve of heart. All data were estimated/run by MATLAB software.

Conclusion: To conclude, this paper aims to bring attention to the clinical reported on geometrical parameters of the mitral valve and the shape of blood fluid across the mitral valve orifice by Bernoulli’s equation and mathematical manipulations.

Keywords: Mathematical Bernoulli Equation; Orifice of the Mitral Valve of Heart; Echocardiography

In the past decade, finite element modeling of complete heart valves has greatly aided evaluation of heart valve surgery, design of bioprosthetic valve replacements, and general understanding of healthy and abnormal cardiac function. Such a model must be based on an accurate description of the mechanical behavior of the valve material. It is essential to calculate velocity/displacement, geometrical indices and strain rate/strain at a component level that is to work at the cellular level. In this study we developed the first three-dimensional mitral valve modeling based on Bernoulli’s equation and mathematical techniques to solve them in the characterization of mitral valve leaflets in continuum equations of inelasticity framework based on echocardiography.

We suggest a problem. A fluid reservoir of circular symmetry is to be designed. The minimum and maximum heights of the reservoir above the ground are h and H respectively. The fluid exits through the mitral valve orifice at H. The time for the fluid to reach a particular height above the ground, say height z, is given by t(z) where t(H) = 0. Determine the shape of mitral valve leaflets [1-5]. The objective of this paper is to study and give an algorithm for the mechanisms of mitral valve of the heart based on mathematical techniques and Bernoulli’s equation based on echocardiographic datasets.

The problem is to determine the shape f(y) of a wire equation notch (here the notch is considered the orifice of the mitral valve and a wire equation is realized by the streamline flow behind the mitral valve and a modeling of mitral valve leaflets), an opening in mitral valve leaflets, in which the volume flow rate of fluid, Q, through the orifice is expressed as function of height h of the orifice [6]. We first establish the equation.

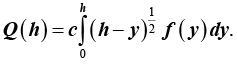
Assuming Bernoulli’s equation can be applied between the point “a” and “y” in Figure 1, we obtain

(*)

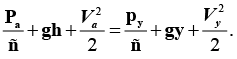
Where P_a, P_y, V_a, V_y are the pressures and velocities at point “a” and “y”; g is the graviational acceleration and ρ is the fluid density [7].

The pressures at “a” and “y” are both taken to be nearly atmospheric so that P_a = P_y and the velocity at “a” is assumed to be negligible (V_a = 0) since the fluid behind the orifice is slow moving. Thus, (*) becomes

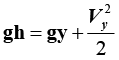
So that

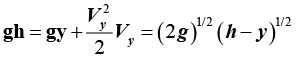
Gives the velocity of the fluid at distance “y” behind the orifice of the mitral valve in Figure 1.
The elemental area (shaded region in Figure 1B) is given by:

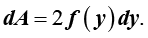
So, by definition, the elemental volume flow rate through dA is

(**)

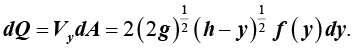
Denoting

by c and integrating (**) from y = 0 to y = h gives the total volume flow rate through the orifice of the mitral valve:

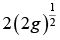
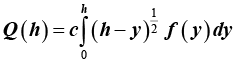
We find f(y) by finding f(h) inversely by the following formula:

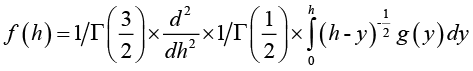
Where

and Γ is the Gama function. Since

is known g(h) and g(y) are known. For the mitral valve with numerical calculations of the leaflets in echocardiography machines, we can consider

approximately. For example for a=7/2 the blood fluid is shaped like parabola for normal mitral valve of the heart. So by these shapes we can obtain a geometrical modeling which are coded and run in the MATLAB software Figure 2 and 3 [8-17].

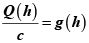
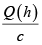
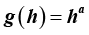
In fact the above formula is a solution of the Lagrange-Euler equations applied to the mitral valve based on echocardiographic datasets

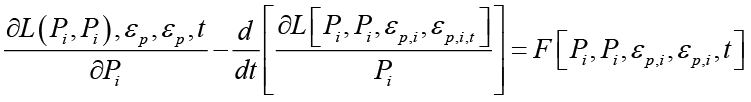
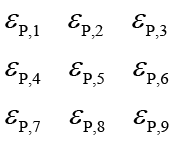
P₁, P₂ ,…, P₉ nine position variables towards 9 strain components

that are made by the speckle tracking method on echocardiographic images ( Figure 2) and L is the Lagrangian which is the kinetic energy mines the potential energy of our system at the vicinity of the mitral valve.

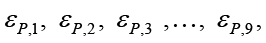
Since

( the length of the tangent line along P) we can rewrite Lagrange-Euler equations as well:

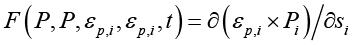
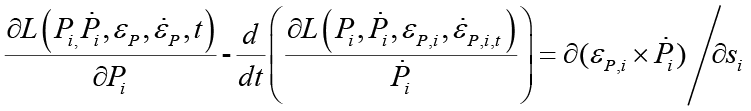
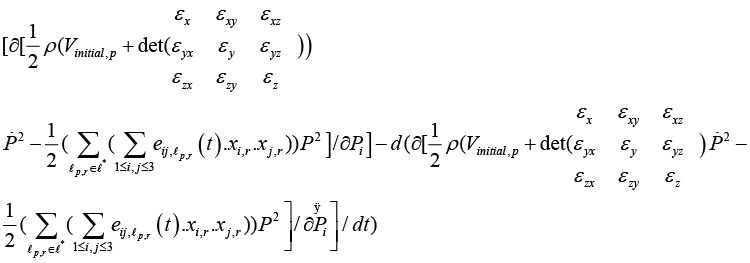
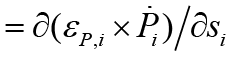
In conclusion, the results of this study suggest that, Bernoulli equation describe explicitly the behavior of the mitral valve leaflets with a huge clinical benefit for physicians and our study also plays a significant role in the transvalvular pressure drop estimation of the mitral valve.